No air currents required: Ballooning spiders rely on electric fields to generate lift

In 1832, Charles Darwin witnessed hundreds of ballooning spiders landing on the HMS Beagle while some 60 miles offshore. Ballooning is a phenomenon that’s been known since at least the days of Aristotle—and immortalized in E.B. White’s children’s classic Charlotte’s Web—but scientists have only recently made progress in gaining a better understanding of its underlying physics.

Now, physicists have developed a new mathematical model incorporating all the various forces at play as well as the effects of multiple threads, according to a recent paper published in the journal Physical Review E. Authors M. Khalid Jawed (UCLA) and Charbel Habchi (Notre Dame University-Louaize) based their new model on a computer graphics algorithm used to model fur and hair in such blockbuster films as The Hobbit and Planet of the Apes. The work could one day contribute to the design of new types of ballooning sensors for explorations of the atmosphere.

There are competing hypotheses for how ballooning spiders are able to float off into the air. For instance, one proposal posits that, as the air warms with the rising sun, the silk threads the spiders emit to spin their “parachutes” catch the rising convection currents (the updraft) that are caused by thermal gradients. A second hypothesis holds that the threads have a static electric charge that interacts with the weak vertical electric field in the atmosphere.

Experimental studies have explored both hypotheses about ballooning spiders. For instance, one 2018 study in Current Biology found that spiders seem able to detect electric fields under natural atmospheric conditions. This triggers ballooning behavior, the study suggests, and the electric fields provide sufficient force to generate lift.

A second 2018 study in PLOS Biology reported on experiments with ballooning crab spiders. Co-author Moonsung Cho, an aerodynamic engineer at the Technical University of Berlin, was inspired after spotting several wild ballooning spiders during a walk through the city’s Lilienthal Park. He and his colleagues constructed an outdoor platform, and one by one, they placed a dozen crab spiders they’d caught onto the platform, videotaping their ballooning behavior. The platforms emitted a fine powder so that the wind’s speed and direction would be visible. They also conducted similar experiments in a wind tunnel, with a reel placed behind the spiders on the platform to spool up sprayed silk lines as if they were fishing line.

Cho et al. found that the spiders seemed to test the conditions before taking off by raising one or two front legs into the air. If the winds were low enough (about 3 meters per second), the spiders would then turn around, stand on “tiptoe,” and raise their butts to the sky. Then they would shoot out several silken threads which formed a triangular parachute. The spiders would anchor themselves to the ground with a drag line during this process and detach themselves only after the parachute began to carry them off.

Cho and his colleagues also determined that the average strand of spider silk measured 9 feet long and a mere 200 nanometers across (less than the wavelength of visible light). At those scales, Cho told The Washington Post, “the air is very sticky, like honey.” He concluded that the combination of sticky air and narrow threads is what gives spiders enough lift to soar through the air.

There have also been simulation studies involving a single thread. However, nobody had yet simulated the effects of multiple threads on ballooning, taking into account the effect of the electrostatic repelling force on the shape of the threads as well as the ballooning velocity. Jawed and Habchi set out to rectify that gap in the literature.

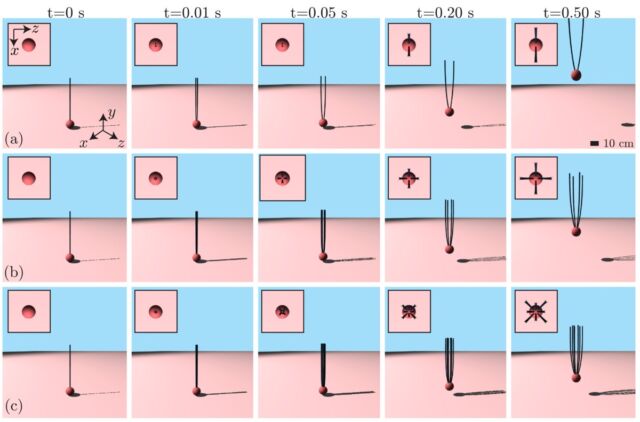
They used an algorithm that essentially divides each silk thread into several segments resembling strands of spaghetti, all of which can bend, stretch, and twist. In true physicist fashion, they modeled an Erigone spider as a sphere, measuring 2 millimeters in diameter. Different variations of the simulation had either two, four, or eight threads attached at the top of the spider-sphere, and the model assumed the threads were coated with electric charges.

Jawed and Habchi also incorporated several other factors into their model: gravity, the atmospheric electric field, the electric charge of the threads, and drag (air resistance) on the threads. Per APS Physics:

In the simulations, the spider starts at rest on the ground and is lifted by the electric field. While the charged, initially straight threads remain attached to the spider, their mutual repulsion causes them to spread apart over a period of time. As the spider accelerates upward, downward drag increases and—combined with the spider’s weight—eventually cancels the lifting force. This competition between upward and downward forces determines a spider’s final (terminal) upward velocity.

The simulations showed that the multiple threads did not become entangled when they were charged. “We think that, at least for small spiders, the electric field, without any help from upward air currents, can cause ballooning,” said Habchi, adding that larger spiders would require a boost from upward airflow. The vertical velocities (8.5 cm/s) were consistent with recent experimental studies, and electric charges distributed uniformly across the thread or merely at the tip were equally capable of generating lift.

DOI: Physical Review E, 2022. 0.1103/PhysRevE.105.034401 (About DOIs).