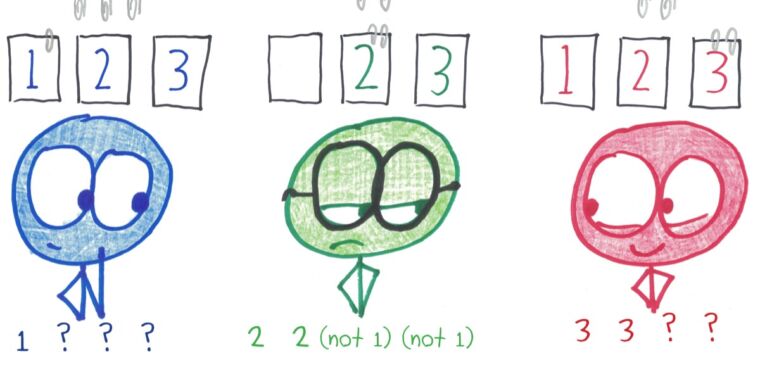
Ben Orlin
Of the thousand games I encountered in researching my book Math Games with Bad Drawings, only one of them truly frightened me. It’s a finger game. But trust me: It is the most cognitively taxing finger game that the human race has yet devised—a cross between a logic puzzle, an improv comedy session, and a collective hallucination, played with the strangest deck of cards you’ve ever seen (or not seen). Keep your aspirin at the ready.
How to play
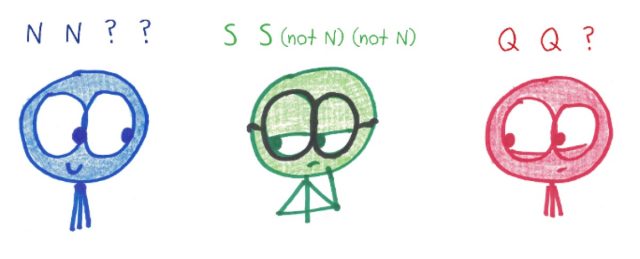
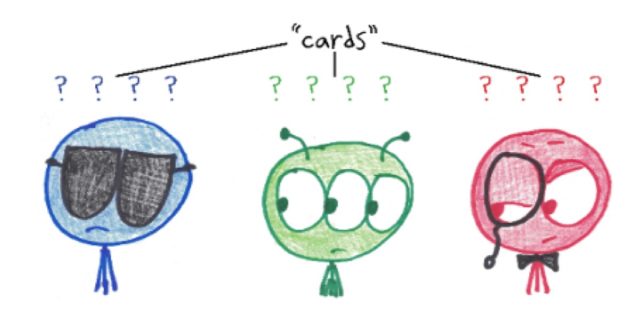
What do you need? Anywhere from three to eight players. Each begins the game by holding up four fingers. These are the “cards” in the deck.

Ben Orlin
What’s the goal? There are two ways to win:
- Prove that you have four cards in the same suit.
- State exactly what suits every player has in their hand.
What are the rules?
To begin, no one knows the suits of their own (or anyone else’s) cards. All is a mystery. We only know that there are four cards per suit and as many suits as there are players.
Ben Orlin
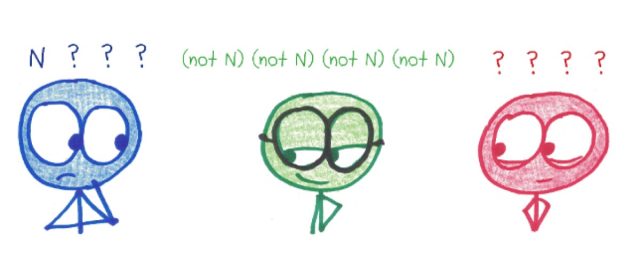
On your turn, pick another player, and ask them if they have any cards from a particular suit. The first person to reference a new suit makes up a silly name for it. Note that you may only ask for a suit you already possess; thus, by asking for Unicorns, you are committing one of your as-yet-unknown cards to being a Unicorn.
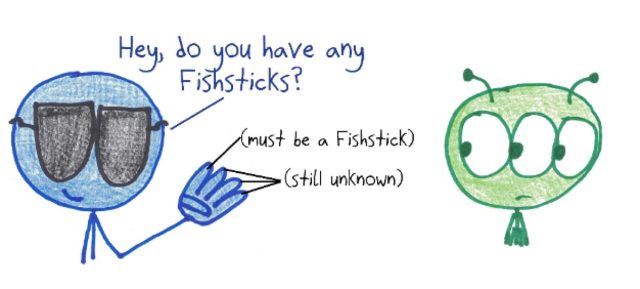
Ben Orlin
The asked player can respond in one of two ways:
- “No, I don’t have any.” Thus, all their cards must belong to other suits.
- “Yes, here is one.” In this case, they give precisely one card to the asking player. Their other cards remain a mystery (and may or may not belong to the same suit).
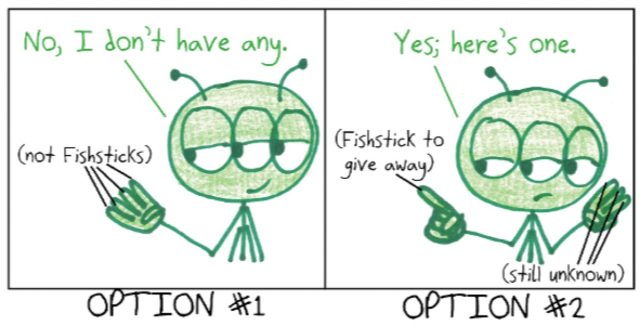
Ben Orlin
Sometimes this decision will be forced. For example, if you’ve already committed to having Radishes, and I ask you for Radishes, then you must give me one. If not forced, the asked player may respond whichever way they wish.

Ben Orlin
You can win in two ways:
- At the end of your turn, state exactly what cards each player must have.
- At the end of your turn, prove that you have four cards in the same suit.
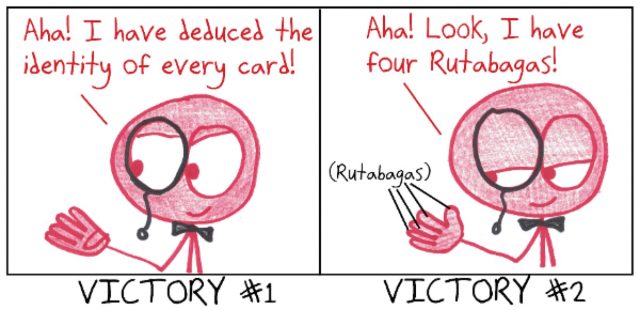
Ben Orlin
However, if a paradox occurs—meaning that the players collectively possess five or more cards all in the same suit and no one caught the error at the time—then something has gone wrong, and everybody loses.
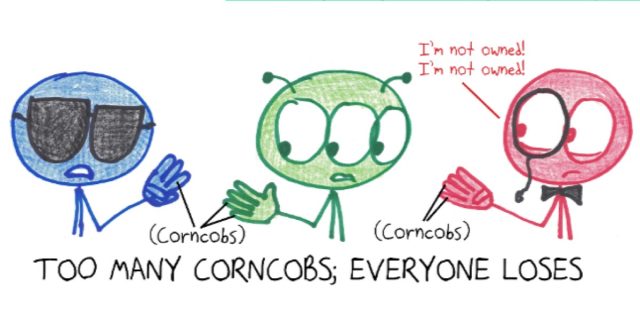
Ben Orlin
Sample round
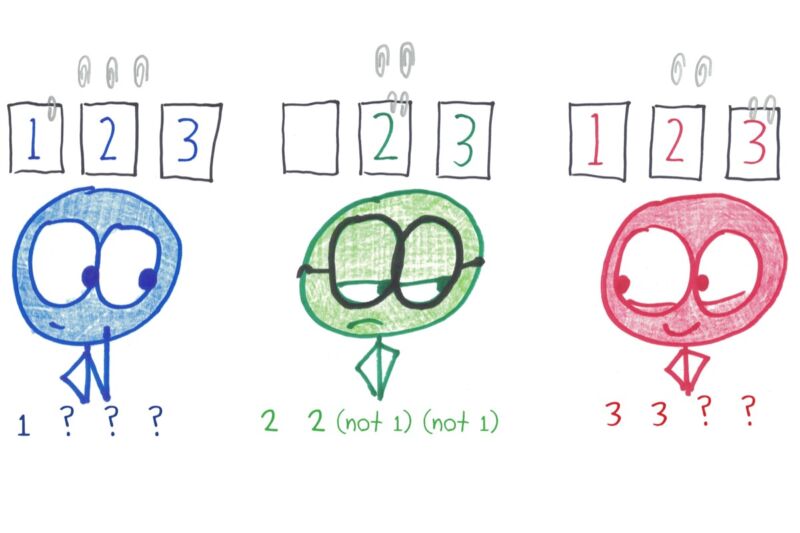
The three players begin with a total of 12 cards: four each of three different suits. No one knows what cards they (or anyone else) have.
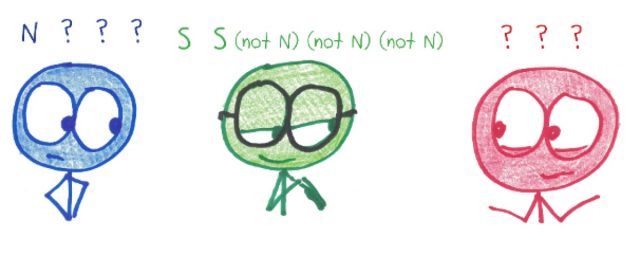
Xia goes first and asks: “Yael, do you have any Narwhals?” Yael chooses to reply, “No.”
Yael goes next and asks: “Zoe, do you have any Scruples?”
Zoe chooses to reply, “Yes.”
The result leaves Zoe with three cards and Yael with five. Of these, two must be Scruples: one implied by asking, and one gained from Zoe.
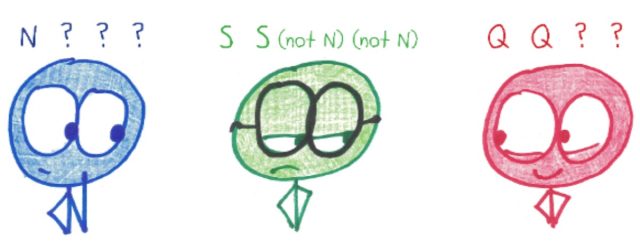
Zoe goes next and asks: “Yael, do you have any Qualms?”
Yael may feel tempted to say, “No.” But this would lead to a game-destroying paradox. Yael has three cards which are not Narwhals; if they’re not Qualms either, then they must be Scruples. That would give Yael five Scruples, which is an impossibility.
Therefore, Yael must say “Yes” and give a Qualm to Zoe.
Xia goes next and asks Zoe, “Do you have any Narwhals?”
Clever move. If Zoe says no, then neither Yael nor Zoe would have any Narwhals. Thus, Xia would have them all and could claim victory. (Some players forbid starting with four cards all of the same suit; under that rule, Zoe would be required to say “yes” here.) Instead, Zoe says “Yes” and gives a Narwhal to Xia, who now possesses at least two Narwhals.
Yael, with the next turn, asks, “Xia, do you have any Qualms?” This means that one of Yael’s remaining cards must be the third Qualm.
Xia chooses to reply “Yes” and gives the final Qualm to Yael. All the Qualms are now spoken for. Moreover, since Yael’s final card can’t be a Narwhal and can no longer be a Qualm, it must be a Scruple.
The next turn falls to Zoe who asks, “Xia, do you have any Scruples?”
This means Zoe’s final card is a Scruple. Indeed, it’s the last Scruple, which means that Xia can’t possibly have one. Why did Zoe even bother to ask?
Because, with all the Scruples and Qualms accounted for, Zoe knows that Xia’s remaining cards are Narwhals. By declaring and explaining this knowledge, Zoe wins the game. (Xia, despite ending the game with all four Narwhals, began with only three, later gaining one from Zoe.) Easy like Sunday morning, right?
Ben Orlin